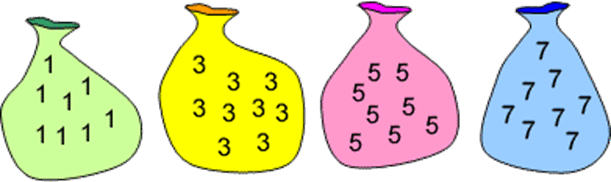Here is a picture of nine of the houses in my street:
Find as many different ways to sort them into groups as you can.
How’d you go?
Problem Solving, as one of the Proficiencies of Mathematics, helps to bring curiosity and creativity to engage learners in Mathematics.
In the Australian Curriculum, The Proficiency of Problem Solving ensures:
Students develop the ability to make choices, interpret, formulate, model and investigate problem situations, and communicate solutions effectively. Students formulate and solve problems when they use mathematics to represent unfamiliar or meaningful situations, when they design investigations and plan their approaches, when they apply their existing strategies to seek solutions, and when they verify that their answers are reasonable.
Strategies students can use to help them problem solve:
P-2/3 Strategies
- Draw – a picture, table or diagram
- Guess – check and improve
- Think – and look for a pattern
- Act – it out and use your hands
- Write – a number sentence
- List – make a list
Years 3-6 use the FISH Strategy
Red Fish - What is the question? What am I asked to find?
Blue Fish – What information do we have? Where is it in the text?
Yellow Fish – What strategies and skills do I have? Does the problem suggest a strategy?
- Guess, check and improve idea
- Look and find a pattern; repetition; sequence
- Work backwards – know the solution
- Draw a picture – model, diagram
- Use a skill – use concrete material
- Solve a simpler problem
- Act it out
- Write a number sentence
- Make a list – table, graph
Green Fish – How reasonable is my answer? How do I know?
See which strategy you use to solve the challenge below.
Age 7 to 11 Challenge Level
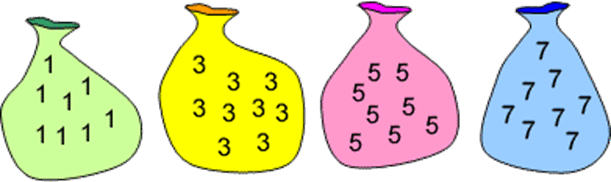
This is a game for two players.
Each bag above has unlimited 1s, 3s, 5s or 7s in it.
Aim of the game:
To be the player to add the final number to the 'running' total to make 37.
How to play:
- Decide who is going first.
- Player 1 chooses one of the numbers from the bags above (1, 3, 5 or 7).
- Player 2 then chooses a number from one of the bags and adds this onto player 1's number to make a 'running' total.
- Player 1 then has another turn and adds that number onto the 'running' total.
- Play continues like this with each player choosing a number and adding it onto the 'running' total.
Things to think about:
- How many numbers did you use altogether in the game?
- Have another go. How many numbers did you use this time?
- What is the largest number of numbers you could use to reach 37?
- What is the smallest number of numbers you could use to reach 37?
- Can you use all the different numbers of numbers in between the largest and the smallest to reach 37?
- What do you notice? Will your noticing/s always be true? Can you explain why or why not?
Fran says "I need to go first in order to win."
Do you agree with Fran? Why or why not?
(Nrich Maths.org)
Mrs Natalie Adler
Assistant Principal Teaching and Learning: Junior